Ciclo lectivo 2018

Bienvenidos al ciclo lectivo 2018

    Este año trabajaremos con el modelo de aula invertida o flipped classroom es un método de enseñanza que consiste en que  el alumno asuma un rol mucho más activo en su proceso de aprendizaje que el que venía ocupando tradicionalmente. A grandes rasgos consiste en que el alumno estudie los conceptos teóricos por sí mismo, en este caso, a través de una plataforma digital como lo es el blog, allí el alumno encontrará los contenidos a estudiar en diversos formatos: tutoriales, vídeos, demostraciones, experimentos sencillos, simuladores, laboratorios virtuales, power point. También tendrán material en formato papel. El tiempo de clase se aprovechará para hacer puestas en común, resolver dudas relacionadas con el material proporcionado, realizar prácticas, transferir lo interpretado a situaciones nuevas. Teniendo en cuenta que ustedes, los alumnos, se han convertido en lo que podemos denominar «e-alumnos», esto es, personas que dentro y fuera de las aulas emplean las nuevas tecnologías como herramientas de aprendizaje.

     Además los alumnos que por diversos motivos no puedan asistir a clase sean capaces de seguir el ritmo del curso y no resulten perjudicados por  su  inasistencia.

     Como principales ventajas se han señalado las siguientes:

a) Incrementa el compromiso del alumnado porque éste se hace corresponsable de su aprendizaje y participa en él de forma activa mediante la resolución de problemas y actividades de colaboración y discusión en clase.

 b) Tienen la posibilidad de acceder al material facilitado por el profesor cuándo quieran, desde donde quieran y cuantas veces quieran;

c) Favorece una atención más personalizada del profesor a sus alumnos y contribuye al desarrollo del talento.

 d) Fomenta el pensamiento crítico y analítico del alumno y su creatividad;

e)Convierte el aula en un espacio donde se comparten ideas, se plantean interrogantes y se resuelven dudas, fortaleciendo de esta forma también el trabajo colaborativo y promoviendo una mayor interacción alumno-profesor;

f) Al servirse de las TICs para la transmisión de información, este modelo conecta con los estudiantes de hoy en día, los cuales están acostumbrados a utilizar Internet para obtener información e interacción (Bergmann y Sams, 2012)

g) Involucra a las familias en el proceso de aprendizaje porque para el  trabajo previo, extraclase, el alumno debe haber cultivado hábitos de estudio, compromiso y responsabilidad.

Herramientas Flipped Classroom ( algunas de ellas aplicaremos a lo largo del ciclo lectivo)

http://formacion.educalab.es/pluginfile.php/36986/mod_book/chapter/3495/Herramientas%20Flipped%20canva.pdf

Programa

Asignatura: Matemática

Curso 3 er año                  

Unidad 1

Revisión de números enteros, ecuaciones. Números racionales. Operaciones: suma, resta multiplicación, división. Potenciación. Radicación. Expresiones decimales: cálculos combinados.Ecuaciones. Notación científica.

Unidad 2

Circunferencia. Elementos. Área. Cuerpos: clasificación: elementos. Teorema de Euler. Área. Cálculo de volúmenes de cuerpos poliedros y redondos.

Unidad 3

Vectores: operaciones. Proporcionalidad numérica: razones y proporciones. Teorema de Thales. Trigonometría. Razones trigonométricas. Resolución de triángulos rectángulos.

Unidad 4

Expresiones algebraicas: significado, operaciones: suma resta, multiplicación, división, regla de Ruffini, teorema del resto. Cuadrado y cubo de un binomio. Factores. Expresiones algebraicas racionales: suma, resta, multiplicación, división.

Unidad 5

Función lineal. Paralelismo y perpendicularidad. Sistemas de ecuaciones de primer grado con dos incógnitas. Resolución gráfica. Métodos de resolución.

Unidad 6

Estadística: clasificación de una variable, variables continuas, tablas de frecuencias, gráficos, parámetros estadísticos: media  aritmética, moda, mediana.

Lectura comprensiva

En el presente ciclo lectivo pondremos énfasis en la lectura comprensiva, para luego, en la clase, poder aplicar lo interpretado a situaciones diversas.

Objeto de la lectura comprensiva

La lectura comprensiva tiene por objeto la interpretación y comprensión critica del texto, es decir en ella el lector no es un ente pasivo, sino activo en el proceso de la lectura, es decir que descodifica el mensaje, lo interroga, lo analiza, lo critica, entre otras cosas.

En esta lectura el lector se plantea las siguientes interrogantes: ¿conozco el vocabulario? ¿Cuál o cuales ideas principales contiene? ¿cuál o cuales ideas secundarias contiene? ¿Qué tipo de relación existe entre las ideas principales y secundarias?.

Una lectura comprensiva, hará que sea más fácil mantenerte actualizado en cualquier tema y esto es clave hoy en día. La lectura comprensiva implica saber leer, pensando e identificando las ideas principales, entender lo que dice el texto y poder analizarlo de forma activa y crítica.

Importancia

Leer comprensivamente es indispensable para el estudiante. Esto es algo que él mismo va descubriendo a medida que avanza en sus estudios. En el nivel primario y en menor medida en el nivel medio, a veces alcanza con una comprensión mínima y una buena memoria para lograr altas calificaciones, sobre todo si a ello se suman prolijidad y buena conducta. Pero no debemos engañarnos, a medida que accedemos al estudio de temáticas más complejas, una buena memoria no basta.

Actitudes frente a la lectura.

a- Centra la atención en lo que estás leyendo, sin interrumpir la lectura con preocupaciones ajenas al libro.

b- Ten Constancia. El trabajo intelectual requiere repetición, insistencia. El lector inconstante nunca llegará a ser un buen estudiante.

c- Debes mantenerte activo ante la lectura, es preciso leer, releer, extraer lo importante, subrayar, esquematizar, contrastar, preguntarse sobre lo leído con la mente activa y despierta.

d- No adoptes prejuicios frente a ciertos libros o temas que vayas a leer. Esto te posibilita profundizar en los contenidos de forma absolutamente imparcial.

e- En la lectura aparecen datos, palabras, expresiones que no conocemos su significado y nos quedamos con la duda, esto bloquea el proceso de aprendizaje. Por tanto no seas perezoso y busca en el diccionario aquellas palabras que no conozcas su significado.

Rubrica de evaluación del desempeño áulico del alumno

Valoración: 0 (no cumplió); 1 (deficiente); 2 (regular); 3 (bueno); 4 (muy bueno)

Criterios	0	1	2	3	4
Tarea extraclase (lecturas, resolución de ejercicios…)
Contesta preguntas del docente y de sus compañeros al momento de hacer la puesta en común.
Presenta argumentos fundamentados en las lecturas y trabajos de la clase.
Demuestra iniciativa y creatividad en la resolución de las actividades solicitadas.
Demuestra entendimiento y comprensión de los temas tratados en clase.
Usa vocabulario específico de la asignatura.
Demuestra asimilación de contenidos  para transferir a situaciones nuevas.
Se dirige en forma respetuosa a sus compañeros.
Usa el celular según lo acordado por la docente.
Escucha y hace silencio cuando corresponde.
Usa correctamente fórmulas y unidades
Sigue adecuadamente las instrucciones (guía) en el momento de trabajar en el laboratorio, aplicando conocimientos previos.

Comenzamos!
Recuerda que de cada material que leas o visualices debes tomar apuntes en tu carpeta para poder participar activamente en clase!

Perímetros y áreas del rectángulo y del triángulo, recuperado de:

https://www.youtube.com/watch?v=wYNvY_bOGdc

Perímetro y área de un  círculo, recuperado de:

https://www.youtube.com/watch?v=iqefaBihj7U


20/03/18

Tema: perímetros y áreas de figuras geométricas 

Perímetro y área del círculo

Toma apuntes de los conceptos fundamentales

Recordemos que circunferencia y círculo son dos cosas diferentes.

La circunferencia es el conjunto de puntos que se encuentran a una misma distancia de otro llamado centro.

El diámetro de un círculo

El diámetro es la longitud de la recta que pasa por el centro y toca dos puntos del borde de un círculo.

Perímetro de la Circunferencia

El perímetro (P)  de la circunferencia es la medida de su longitud. Se puede obtener de dos maneras:

1).- Multiplicando “pi”,  que se simboliza (π)  y su valor es 3,14 por diámetro (d)

 Ecuación:           P =  π x d

Veamos un ejemplo.
Obtener el perímetro de la circunferencia del siguiente círculo (la longitud de la línea verde punteada).

Aplicando la ecuación:

P = π x d

P = 3.1416 X 8 cm
P = 25.1328 cm

El radio de un círculo

Observa que un diámetro está compuesto por dos radios:

Así, el diámetro (d) de un círculo es dos veces su radio:

d = 2r

2).- Otra forma de calcular la longitud de la circunferencia es: multiplicando dos veces “pi” por el radio

Ecuación:                              P =  2π x r

Por ejemplo, si el radio es de 4 cm

Aplicando la ecuación (recuerda que el radio es igual a la mitad del diámetro).

P =  2π x r

P =  2(3.1416) x 4 cm

P =  6.2832 x 4 cm

P =  25.1328 cm

Círculo

El círculo es la superficie que queda limitada por la circunferencia.

Área del círculo

El área del círculo es la medida de su superficie, como se trata de dos dimensiones, el resultado se da siempre en unidades cuadráticas o cuadradas.

El área del círculo se obtiene con la fórmula: pi por radio al cuadrado.

A =  π x r²

Veamos un ejemplo.
Obtener el área del siguiente círculo (la superficie amarilla).

A =  π x r²

A = 3.1416 x (4cm )²

A = 3.1416 x 16 cm²

A = 50.2656 cm²

PERÍMETRO Y ÁREA DEL CUADRADO

	PERÍMETRO   El perímetro de un cuadrado es cuatro veces el valor del lado     P = 4 · a
	ÁREA El área de un cuadrado es igual al cuadrado de la longitud del lado.   A= a2

PERÍMETRO Y ÁREA DEL RECTÁNGULO

	PERÍMETRO El rectángulo tiene los lados iguales dos a dos, por tanto: P = 2· a + 2· b
	ÁREA El área de un rectángulo es el producto de la longitud de los lados. A= a · b

Ejercicios

1.- Calcula el perímetro y el área de un cuadrado de lado 4 m. 2.- La base de un rectángulo es 5 m. y la altura la mitad de la base. Calcula el área y el perímetro. 3.- El área de un cuadrado es 5,76 cm2 . Calcula el perímetro del cuadrado. 23/04/18 Perímetro y área del trapecio, rombo y romboide. Perímetro del Trapecio Recordemos que el trapecio puede ser rectángulo, isósceles o escaleno. Clasificación Dependiendo de las medidas de los ángulos internos los trapecios se dividen en tres tipos o grupos: - Trapecio Rectángulo: Tiene un lado perpendicular respecto a ambas bases. En consecuencia el lado restante posee un ángulo agudo y el otro obtuso. - Trapecio Isósceles: Posee los lados no paralelos de idéntica longitud. En cuanto a sus ángulos son dos agudos y dos obtusos iguales entre sí. - Trapecio Escaleno:  poseen lados con diversas longitudes entre sí y también con los cuatro ángulos diferentes. a).- Perímetro del trapecio El perímetro del trapecio es igual a la suma de los valores de sus cuatro lados. Por lo que la fórmula queda así: P = L +L+L+L Ejemplo: Areas del  trapecio El área de un trapecio se calcula a partir de su altura y los dos lados paralelos (a y b) o bases del trapecio. Rombo El perímetro de un rombo es cuatro veces la longitud de uno de sus lados (a), ya que tiene sus cuatro lados iguales. P = 4 . a             siendo (a) un lado del rombo. Ejemplo: P = 4 . 5 cm = 20 cm Area El rombo es un paralelogramo (que tiene los cuatro lados iguales) Para hallar el área la expresión más habitual es en función del valor de sus diagonales, que son perpendiculares entre sí. Por tanto el área del rombo es : D es la diagonal mayor, d es la diagonal menor. Romboide El perímetro de un romboide es la suma de sus cuatro lados. Como el romboide tiene los lados iguales dos a dos, su perímetro es el doble de la suma de los lados diferentes (a y b). Ejemplo Supongamos que tenemos un romboide siendo sus lados conocidos e iguales dos a dos, donde dos son de longitud a=4 cm y los otros dos b=8 cm. P = 2 ( a + b)  P = 2 ( 4 cm + 8 cm) = 24 cm Area del romboide El área será el producto del lado b y su altura h: A = b . h A = 10 cm . 4 cm = 40 Cm2

Vídeos
1) Área del trapecio
https://www.youtube.com/watch?v=P3jLLjDBm6w

5/05/18
1)Teorema de Pitágoras
Se aplica a triángulos rectángulos
Pasar a ver los siguientes vídeos y tomar apuntes de los conceptos fundamentales, recuperados de:

https://www.youtube.com/watch?v=w6nh99v3r4A

2) Calculo del área de un polígono regular:

https://www.youtube.com/watch?v=B9nIjZgvluk

3) Teorema de Pitágoras aplicado a figuras planas:

https://www.youtube.com/watch?v=WXRdDDo1xbA

14) Volumen de cuerpos geométricos (luego edito material)

14/05/18
Volumen

Relación de volumen de pirámide y prisma
https://www.youtube.com/watch?v=8tf_2lyyWoM

Cuerpos de revolución
https://www.youtube.com/watch?v=kD5gz2k5IZQ

Ecuaciones para calcular volúmenes
https://www.youtube.com/watch?v=2Cq-N5DDNg4

Práctica sobre volumen (copiar o imprimir)

1-¿Cuántos peces, pequeños o medianos, se pueden introducir en un acuario cuyas medidas interiores son 88 x 65 x 70 cm? (Se recomienda introducir, a lo sumo, un pez mediano o pequeño cada cuatro litros de agua)

2-a) de la ecuación de cilindro despejar altura.

b) Se echan 7 cm³ de agua en un recipiente cilíndrico de 1,3 cm de radio. ¿Qué altura alcanzará el agua?

3-¿Cuántos cilíndricos, de 47 cm de altura y 16 cm de radio, se tienen que vaciar en una piscina de 10x6x1,5 m para llenarla?

4-¿Cuántas copas se pueden llenar con 6 litros de refresco, si el recipiente cónico de cada copa tiene una altura interior de 6,5 cm y un radio interior de 3,6 cm?

5-Se introduce una bola de plomo, de 1 cm de radio, en un recipiente cilíndrico de 3,1 cm de altura y 1,5 cm de radio. Calcula el volumen de agua necesario para llenar el recipiente.

6- Calcula, en litros, el volumen de un tetrabrik cuyas dimensiones son 12x7x15 cm

7-Durante una tormenta se registraron unas precipitaciones de 80 litros por metro cuadrado. ¿Qué altura alcanzaría el agua en un recipiente cúbico de 10 cm de arista?

8-Un pantano tiene una capacidad de 450 hm3 . Si actualmente está a un 76% de su capacidad, ¿cuántos metros cúbicos de agua contiene?

9-. Me han encargado 6 litros de refresco de naranja. En la tienda sólo quedan botellas de 250 cl. ¿Cuántas tengo que comprar?

10-¿Cuántos vasos cilíndricos de 19 cm de altura y sus bases son 6,1 cm y 3,8 cm. 2,7 cm de radio se pueden llenar con 3,8 litros de refresco?

11-¿Cuántos bloques cúbicos de piedra, aproximadamente, de 50 cm de arista, hacen falta para construir una pirámide regular con base cuadrada de 208 m de lado y 101 m de altura?

12-Calcula, en litros, el volumen de un cono que tiene 12 cm de altura y cuya base tiene un radio de 5 cm.

Dato para recordar : equivalencia entre unidades de capacidad y volumen ( 1 litro = 1 dm³)
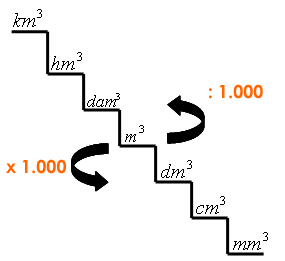
Aquí les dejo las unidades de volumen:

22/05/18

Razones y proporciones

Visualizar y anotar los conceptos fundamentales, recuperado de:

https://www.youtube.com/watch?v=CWd83SreAp0

26/07/18
Hola les dejo los siguientes links para visualizar como funcionan : go Animate; BigHugeLabs, son soportes online que permiten hacer vídeos animados:
GoAnimate

1) https://www.youtube.com/watch?v=Wxch7vl4CcU
2) https://www.youtube.com/watch?v=xII1hoY2TlI
3) https://www.youtube.com/watch?v=bbkgtk2qlzE

BigHugeLabs
1)https://www.youtube.com/watch?v=QrBUMY2QrtI&t=78s

Aquel que quiera, ingrese a GoAnimate , puede registrarse y probar como funciona según lo visto en el vídeo.

Otro recurso es Power Point
https://www.youtube.com/watch?v=pdXBZa7iEZU

Expresiones algebraicas: Polinomios
Suma de polinomios, recuperado de:
https://www.youtube.com/watch?v=FoRrDsGm2EQ


Resta de polinomios,recuperado de:
https://www.youtube.com/watch?v=nzbNxrWH_Rs

Multiplicación de polinomios,recuperado de:
https://www.youtube.com/watch?v=xRC447bTueU&t=288s


División de polinomios,recuperado de:
https://www.youtube.com/watch?v=XYNruwyOY_s

https://www.youtube.com/watch?v=LZj1a-MURP8

Regla de Ruffini (otra forma de dividir) recuperado de:

https://www.youtube.com/watch?v=t8yrL3OFtRo

Raíces o ceros de un polinomio aplicando Ruffini, recuperado de:
https://www.youtube.com/watch?v=GyppFAFxBVc&t=25s